
The architect of stadiums from Izmir
Selin Özaşık, a graduate of the Department of Architecture at Izmir University of Economics (IUE), was selected to join the ...
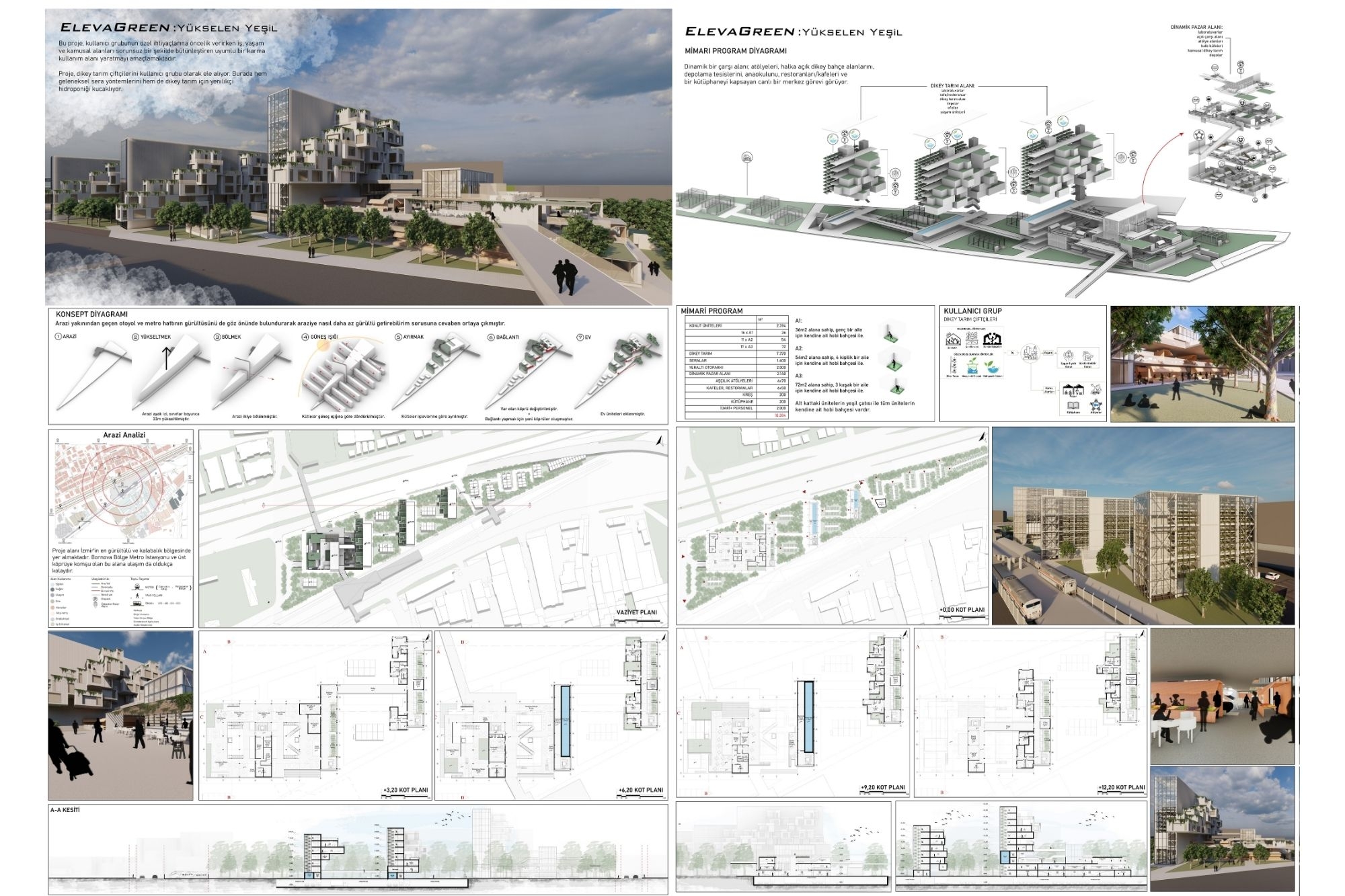
Our 2023 Graduate Ceyda Coşar is among the winners of the SMD Students' Graduation Project Award
Our 2023 graduate Ceyda Coşar has won an award at the İZMİR SMD Student Graduation Project Awards. ...

They examined building, showcased their models
Izmir University of Economics (IUE) Department of Civil Engineering and Architecture students examined 58 buildings in Izmir in terms of ...

They produced ‘vegan leather’ from olive pulp
Olive, which is one of the values unique to the Aegean and has been an indispensable element of tables for ...

‘Bacterial cellulose’ in fashion
Filiz Özbengi Uslu, Gözde Damla Turhan and Selen Çiçek from Izmir University of Economics (IUE) Faculty of Fine Arts and ...

"The Nature of Architecture"
The Department of Architecture hosted Landscape Architect Artem Piskunov ve Architect Ahmed Al-Ali within the context of the "the Nature ...

‘Became the first Turk registered to the Portuguese Chamber of Architects’
Bengisu Özpirinççi (32), graduate of Izmir University of Economics (IUE) Department of Architecture, established her own brand in Portugal, where ...


































